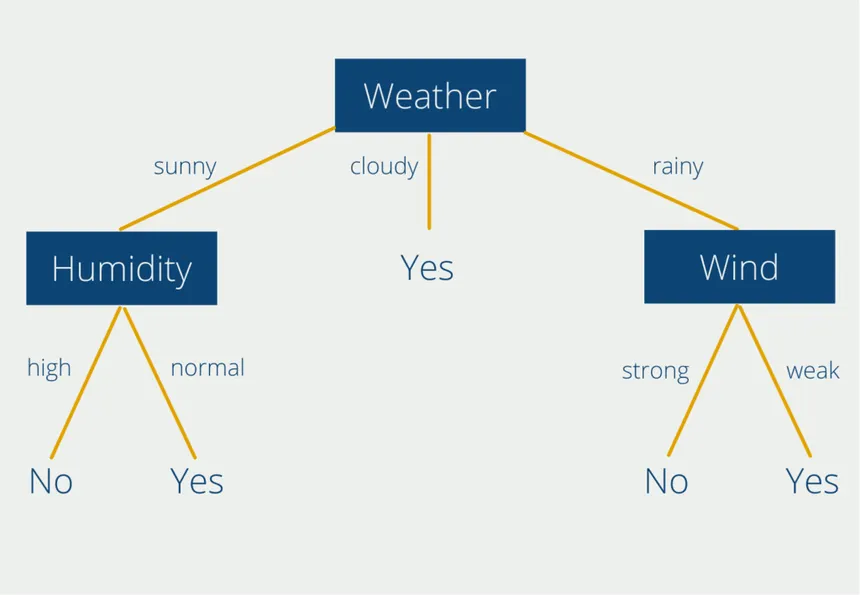
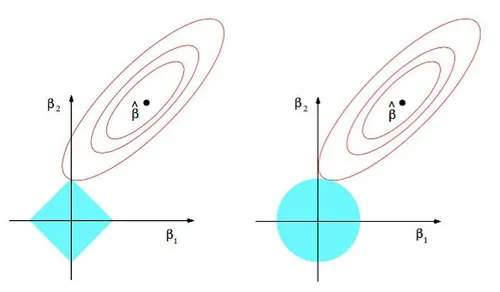
Introduction to Machine Learning
This section provides a high-level overview of machine learning, establishing the core goal of generalization and introducing the main paradigms of learning. It sets the stage for understanding not just what ML is, but why it's structured the way it is. If you want to refresh your math fundamentals before diving into this click here - Math Fundamentals (RECOMMENDED)
1.1. What is Machine Learning?
At its core, Machine Learning is the science of getting computers to act without being explicitly programmed. Instead of writing a fixed set of rules, we provide algorithms with large amounts of data and let them learn the rules and patterns for themselves. The formal definition by Tom Mitchell provides a more structured view:
"A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E."
Let's break this down with a real-world example: a spam filter.
- Task (T): To classify emails as either "spam" or "not spam".
- Experience (E): A massive dataset of emails, where each one has already been labeled by humans as spam or not spam.
- Performance (P): The percentage of emails the program correctly classifies.
The ultimate goal is generalization: the ability of the model to perform accurately on new, unseen emails it has never encountered before, not just the ones it was trained on.
1.2. The Pillars of ML
Supervised Learning
Think of this as learning with a teacher or an answer key. The model is given a dataset where each data point is tagged with a correct label or output. The goal is to learn a mapping function that can predict the output for new, unseen data. It's like a student studying flashcards where one side is the question (input) and the other is the answer (label).
Unsupervised Learning
This is learning without an answer key. The model is given data without explicit labels and must find structure or patterns on its own. A common task is clustering, or grouping similar data points together. Imagine being given a box of mixed Lego bricks and you sort them into piles based on their shape and color without any instructions.
Self-Supervised Learning
This is a clever type of supervised learning where the labels are generated from the input data itself. For example, you could take a sentence, remove a word, and then train a model to predict that missing word. The "label" is the word you removed, but you didn't need a human to create it. This allows models to learn from vast amounts of unlabeled text or image data.
Reinforcement Learning
This is learning through trial and error, like training a pet. An "agent" (the model) learns to make decisions by performing actions in an "environment" to maximize a cumulative reward. It learns from the consequences of its actions, receiving positive rewards for good actions and penalties for bad ones.
1.3. The ML Workflow
Nearly every machine learning project follows a standard, iterative lifecycle. Understanding these steps is crucial for building effective models.
- Problem Framing: Define the objective. What question are you trying to answer? Is it a regression problem (predicting a number) or a classification problem (predicting a category)? What metric will define success?
- Data Collection & Preprocessing: Gather the necessary data. This is often the most time-consuming step, involving cleaning the data (handling missing values, outliers), feature engineering (creating new input signals), and scaling features to a common range.
- Model Selection & Training: Choose a suitable algorithm and feed it the prepared training data. The model learns the underlying patterns during this "training" phase.
- Evaluation: Assess the model's performance on a held-out test set—data it has never seen before. This gives an unbiased estimate of how it will perform in the real world.
- Hyperparameter Tuning: Adjust the model's settings (hyperparameters, like the 'k' in k-NN) to improve performance, often using a validation dataset to prevent overfitting to the test set.
- Deployment: Integrate the trained model into a production environment where it can make predictions on new, live data.